Innovative integrated magnetic for DAB power converter

DAB converters are more and more used on power and/or energy storage systems because they offer bidirectional power transfer, galvanic insulation, and above all higher efficiency and better power density than classical topologies. They can be used on aerospace power network, on-board batteries charging, or to provide high voltage DC bus for motor inverters or plasma thrusters. DAB require an inductor in series with a transformer. 

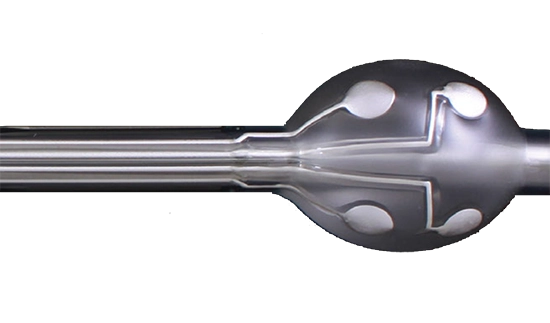
This article presents an innovative integrated magnetics, which gather inductor and transformer functions in a single component. This integrated magnetic component offer high power density and meet high switching frequencies requirements. For example, a component of less than 250g, more than twice as light as two discrete components, is able to transfer 2kW at 300kHz with an efficiency close to 99%. These integrated components are intended for power converters from a few kW to a few hundred kW, and operating at several hundreds kHz. The use of integrated magnetics make the manufacturing easier, decrease volume and weight, and increase the reliability by reducing the number of components.

This component is the result of a double optimization with the 3D finite element simulation software FLUX :

• Reducing the magnetic circuit while increasing and controlling leakage inductance,
• Reducing copper losses due in large part to Eddy currents, proximity effects and circulating currents.

In general, an increase in leakage inductance tends to increase Eddy currents. The innovative and ambitious part of this work was to reach increasing leakage while reducing Eddy currents. Another tricky part of this work was to find a good compromise between accuracy of Eddy current loss calculations and resolution times associated with sizes of the mesh. In a last step, simulations results were compared to and validated by experimental measurements.

INTRODUCTION

Reducing carbon footprint is one of today's major challenges. E-mobility is a powerful lever for achieving this goal, but it requires the management of high electrical power while controlling weight.
This will only be achieved by using innovative power architectures involving higher frequencies and higher voltages.

Power magnetic components are key in the operation of power converter.
The use of high-frequency, high-power innovative conversion architectures requires the development of specific magnetic components to achieve the desired performance. At high frequency, leakage flux and parasitic capacitance can strongly affect power supply operation and needs to be mastered.
Specific technologies have been developed to control and leverage the magnetic flux in order to integer the series inductor the required by most of these new architectures, into the transformer, while maintaining high efficiency.

This paper concerns the dual active bridge architecture but the integrated magnetic component meets as well the requirements of LLC and coupled inductors used in interleaved converters.
The dual active bridge has been chosen because it is one of the most promising architecture for the management of electric power thanks to its bidirectional operation, soft switching, and the additional control parameter with phase shift between inverter and rectifier.

INTEGRATED MAGNETIC COMPONENT (IMC) CHARACTERISTICS

The first step to meet high frequency requirements is the reproducibility of leakage flux and parasitic capacitances. This was achieved by using winding technologies based on copper strip or plate conductors hold in position by specific bobbins.

A leakage inductance high enough to meet the serial inductor values needed by innovative architectures requires a significant increase in the leakage flux between the windings. This magnetic field may generate high Eddy current losses in conductors and must be channeled by using specific magnetic configurations.

Controlling inductance values requires the use of air gaps in magnetic cores, which can generate fringing magnetic field that also lead to eddy current losses in nearby conductors. Distributed air gaps have been used to mitigate this phenomenon.
High currents at high frequencies while reducing the volume should lead to use several conductors in parallel. This solution has to be used carefully because any difference in length or magnetic flux across parallel coils results in high circulating currents and inhomogeneous distribution of average current.

The aforementioned items are the key factors to design and optimize an integrated magnetic component at the considered current and frequency level.
The analysis carried out quickly showed the limitations of analytical methods, which can only be used to asses losses in very specific geometries. Finite-element simulation is necessary, but requires that the phenomena can be modeled and simulate accurately.

MODELING AND SIMULATION DIFFICULTIES

Modeling these phenomena is therefore essential for component optimization.
Mesh size is a critical point of simulation because it has to be fine enough to model skin effect and eddy current in conductors, but large enough in less critical areas to reduce calculation times. In the same way, 2D simulation should be preferred to 3D simulation as long as the results remain accurate enough.
One of the main difficulties was to identify a mesh that met the above constraint. Traditional automatic meshing using triangles (2D) and tetrahedrons (3D) over the entire discretized surface (2D) or volume (3D) is not suitable. We used extruded squares or cubes.
What's more, in a number of eddy current cases, the traditional law of 2 meshes in the skin thickness is not sufficient. For example, in the case of a conductor facing an air gap, eddy currents appear at frequencies well below the skin thickness. Finally, the surfaces/volumes where we assumed current densities could vary greatly were divided, in order to limit the areas in which the mesh was refined.
All these precautions were not enough to obtain reliable results within an acceptable resolution time. We used a new solver developed recently called the “FE method for calculating facet J0 and edge Tjw (J0=J0f + rot Tjw)”. The principle of this solver is to compare the current densities J from one mesh to another. If the variations, mathematically called gradients, are abrupt and/or discontinuous from one mesh to the next, the values are wrong. The solver then modifies the values with a compensation law. We tested this solver by comparing the loss results obtained on two examples: one with a coarse mesh and the new solver, the other with a highly refined mesh. On both examples, the difference was few %, while the resolution time was much shorter with the coarse mesh.
Another tricky aspect is to take into account the distribution of average currents in parallel turns. With the electrical/magnetic coupling via circuit equations, the software used was perfectly suited to this task. Other programs, such as FEMM, require iterative resolution to make the voltages at the terminals of each parallel turn identical.

QUICK ANALYSIS OF DAB FUNCTIONING

The meshing method being defined, the power converter should be analyze to reproduce its operation.
The losses considered come from the circulation of currents in the conductors. It is therefore essential to reproduce the currents flowing in the component during power supply operation, and in particular to respect the phases of the primary and secondary currents. In fact, the phase has a major influence on any compensation of ampere turns, significantly modifying the magnetic fields present close to the windings.

The dual active bridge architecture has been chosen for the optimization of the integrated magnetic component. This converter consists of an inductor in series with a transformer between two full bridges:
 

Figure 1: Dual Active Bridge architecture

This architectures offer several control strategies based on the duty cycle, phase shift between the two full bridges or a combination of both. Phase shift control has been chosen for its simplicity, as the aim of this study is not to optimize the power converter, but to concentrate efforts on the magnetic components.
Without phase shift between the two bridges controls, synchronous scare-wave voltages are generated on both sides of the inductor. Thanks to the transformer, these voltages have the same magnitude, and no current flows through the inductor. Therefore, no power transits through the converter.

Figure 2: Voltages and inductor current waveforms without and with phase shifts

A positive phase shift generates a voltage across the inductor leading to a current and a power transfer from input to output. A negative phase shift will lead to a power transfer from output to input.

CHARACTERIZATION OF THE IMC

The first step before simulating the operation of the dual active bridge is to calculate the leakage and magnetizing inductances from finite element simulations. According to the method developed by Zaikin and Denys, three simulations are required to calculate these parameters.

ZAIKIN, DENYS (2023): Extraction of Transformer Parameters from FEMM Simulations and Automated Creation of a Transformer SPICE Model Using a Scripting Language. TechRxiv. Preprint. https://doi.org/10.36227/techrxiv.22263358.v4

The first simulation consists in supplying the primary winding only with a current generator, leaving the secondary unloaded. The second consists of supplying the secondary winding only with a current generator, leaving the primary unloaded. The third is to supply primary and secondary windings with current generators in phase opposition to cancel the magnetic field. The inductances values can be deduced from these three simulation results, which are linearly independent from a mathematical point of view. The fine conductor meshing required to accurately model high frequency Eddy current phenomena considerably increase the calculation times, and the 3D simulation have had to be abandoned. The depth of the 2D model has been adjusted to compensate the lack of return magnetic path and get the right leakage inductance value, which represents the serial inductor of the dual active bridge.
Remember that characterizing a two-winding transformer requires the determination of 3 parameters. We have chosen 1 series inductance, 1 parallel inductance and 1 transformation ratio, as shown in figure 3 below.
The key factors for integrated magnetic component optimization are losses generated by the high currents at high frequency. Then the most suitable and the easiest way to supply the model is the use of current generators. Considering the following basic equivalent circuit, two current generators can supply the model.

 

Figure 3: Current supply of integrated magnetic component

If the input and output currents are in phase, there is no current in the magnetizing inductor, no voltage between its ends, and therefore no power transferred from input to output. Phase shift between input and output current lead to energy transfer and allows controlling its flow and direction.
It also controls the voltage across the magnetizing inductance and therefore the primary and secondary voltages of the transformer.
The first step to reproduce the operation of the dual active bridge is to set the currents at their nominal values. The second step consists in tuning the currents phase shift to reach the nominal voltage at the primary/secondary sides of the transformer.

Figure 4: Primary (purple) and secondary (green) voltages versus current phase shift Rated voltages were achieved with a phase shift of 2.11 degrees.

With currents and voltages identical in amplitude and phase, dual active bridge operation is accurately reproduced. This was verified by calculating the output power corresponding exactly to nominal value.
The disadvantage of this method is its high sensitivity to the value of the phase shift. This value is small but has to be very accurate to operate at the right voltages.

EXPERIMENTAL RESULTS WITH THE MANUFACTURED IMC

The aforementioned methods have been used to optimize an integrated magnetic component for a 2kW Dual Active Bridge 270V/28V operating at 300kHz.
Figure 5 below shows the waveforms obtained on the DAB model with the integrated magnetic component. They are conventional.

 

Figure 5 : Voltage and current waveforms of the DAB with the IMC

The optimized magnetic component part has been successful evaluated at nominal operation. Main features:
Volume: 85 cm3 Weight: 250g
Losses < 20W at nominal power
Operation at room temperature without heat sink

Figure 6 below shows the difference between the initial 2 discrete magnetic components used in the DAB, and the final version of the IMC designed. The Integrated Magnetics is 2 times more compact and lighter than the 2 discrete ones.

Figure 6 : Shapes of 2 discrete magnetic components (up) compared to final IMC (down)

Information on the construction and technical solutions used to achieve these performances is not detailed here in order to preserve confidentiality. Further information will be provided during the presentation.

Benoit Krafft ⁽¹⁾, Bruno Cogitore ⁽²⁾
(1)    EXXELIA
16 parc d’activités du Beau Vallon, 57970 ILLANGE, FRANCE
(2)    EXXELIA
137 rue de Mayoussard, ZA de Centr’Alp, 38430 MOIRANS, FRANCE